What are Volumetric or 3D Textures?

Volumetric Textures, 3D Textures or Solid textures (these 3 names will be used throughout the text) are a logical extension of 2D textures. 2D textures (the ones we know already) are images, two dimensional flat images. These 2D texture maps are defined by an array of texels which is nothing more than a rectangular group of colored pixels. 3D textures are, as the name suggests, three dimensional - no longer flat but volumetric (hence the name). The texels now become unit cubes (volumes - sometimes referred to as voxels - I won't use the term voxels since I think it might confuse people about what 3D textures really are) in texel space thus colors in a cubic group not just a flat rectangular array. The 3D texture map texels are packed into a rectangular parallel pipe, each dimension constrained to be a power of two. This is just like 2D texture maps which also have square sizes: 64x64, 128x128, etc. For volumetric textures we just add another dimension and we get, for example, 64x64x64 or 128x128x128.

As I said before, this 3D texture map occupies a volume rather than a rectangular region, and is accessed using three texture coordinates S, T, and R (only S and T are used in 2D textures). As with 2D textures, texture coordinates range from zero to one in each dimension. Now, this might not be very clear to you so let me explain what this means by starting from 2D textures and extending that principle to 3D textures.

Texture maps are used to add surface detail to polygon models (3D objects are modeled using polygons, usually triangles). This is done by applying a texture map (an image, if you will) to the surface. This application is a bit like wrapping the texture around the object, so kind of like gift wrapping a present. This wrapping is done using texture coordinate, the coordinates S and T. Now, don’t worry about the coordinates names they are just labels like we normally use X and Y in general math. S and T are used to select texels (pixels) inside the texture map. Lets assume that S is used to define the horizontal position and T is used for the vertical position (so S is equivalent to X and T is equivalent to Y). Now, when defining a 3D model you don’t just need to define its shape (vertices -corners- of the triangles forming the 3D model), you also need to specify texture coordinates, so you need to give S and T coordinates. These coordinates give the link between the triangle in 3D space and the texture map. The image below shows a triangle in 3D space on the right and a texture map on the left. The texture map has its S and T axes indicated and the values on these axis go from 0 to 1. For the horizontal S axis the value 0 indicates the left border of the Map while a value of 1 indicates the right border of the Map. The same principle is used for the vertical T axis, bottom is 0 and top is 1. Now, if you want to define a texel (pixel inside the texture map) you specify a (S,T) coordinate set. An example of this is given below by the arrows, the arrow link the vertices to the texture map. These coordinates are only provided for the vertices of the polygon, the positions in between are interpolated (again maths, also perspective correction comes into play which is more maths and outside of the scope of this article).

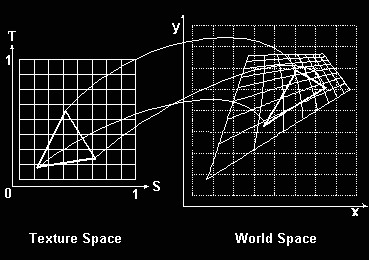
Now, the smart reader is probably wondering about those (S,T) coordinates- how are they generated? Well, a lot of mathematics and projection techniques are involved with this and this is beyond the scope of this topic. Let me just say that finding the correct coordinates is not always an easy task, often this can be quite problematic resulting in distortions. Let me give you a real world example that will convince you of how problematic this mapping can be. Imagine gift wrapping a football (Is this a football football or a soccer ball?? -- Dave). I am sure you understand that its not easy at all to fix a flat rectangular piece of gift paper on top of a spherically shaped ball (soccer --Dave)! You’ll find that the paper is crumbled up at various positions, these ripples are the distortions I talked about. On the other hand wrapping paper around a cube, quite easy. But lets continue.