Looking for Bottlenecks-CPU Clock&putting it all together
This portion will be rather brief, since to be honest there's not much to see: whether by our evil design or a twist of fate (we'll let you figure out which one is which), the scenario we've used for this investigation is rather impervious to the CPU's clock:
Staring at straight lines is rather boring, is it not? We won't compute the fractions affected by the CPU, due to the rather obvious lack of relevance in context (staring at zeroes is equally boring).
Now, we're in a position to draw a few conclusions/fit things in a semi-coherent image:
Finally, if you look at the fractions shown along the way, they help to outline something that's usually lost in the background noise: graphics represent an intricate lattice of intertwined elements that are bound by different factors, and within the confines of a single frame you can be constrained by engine (and many intra-engine factors), memory or even CPU performance, so dealing in absolutes is definitely not the way to go about it.
The fact that Cypress not as limited by VRAM bandwidth as we initially guessed, at least in its 5870 incarnation, can be (simplistically) explained by games typically having an elevated arithmetic intensity (FLOPs/byte ratio). Whilst both the amount of bytes needed to generate one pixel has been increasing itself, the number of computations needed to get the final colour for that pixel has been increasing at a faster pace. Of course, there's more to graphics rendering than pure FLOPs, but in general the weight of on-GPU operations in rendering workloads has been constantly increasing, so if we substitute FLOPs/byte with GPU ops/byte we're probably closer to a more accurate depiction. That's not to say that bandwidth isn't relevant, with its impact being more pronounced as we move to higher levels of AA - whilst it would be nice to assume perfect colour/Z-compression, and thus AA having no cost in bandwidth or compute, practice indicates that's not quite the case, thus making it quite relevant for such scenarios (look at how the fractions affected by the memory clock increase as we add more AA).
We expect the above to hold for 3D rendering in general, but compute workloads are something of a different affair, and one we'll deal with somewhat later, once drivers and SDKs mature a bit and we get everything in place. We'd not be surprised if many compute kernels will be limited by bandwidth before being bound by Cypress' FLOPs.
A nice and simple way of visualising this would be the custom representation of the Roofline Model [Patterson, Williams, 2008], which seeks to put arithmetic intensity, bandwidth and floating-point performance together on a single 2D graph, which looks something like this:
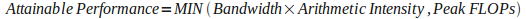
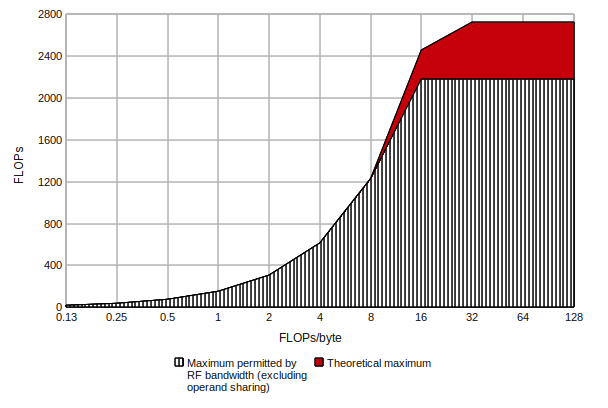
As is obvious, there are a number of simplifications involved, and we're disregarding the impact of caching, taking into account only (theoretical) VRAM bandwidth. On another note, this is an idealised representation: if your nom de plume isn't prunedtree, seeing 2.72 Teraflops from Cypress in actually useful codes is as likely as seeing Dave Baumann crushing his Xbox 360 with a hammer and deleting his Live account.
If we were to place modern game graphical workloads somewhere on that chart, they'd be somewhere to the right, in the [4,16] FLOPs/byte interval - not quite the unachievable pure math nirvana, but not that heavily constrained by bandwidth. We expect games to continue their slow rightward migration in the near future. Compute codes can theoretically be anywhere, but if you're not doing at least more than 2 FLOPs/byte, you may want to consider using the CPU rather than the GPU.
Staring at straight lines is rather boring, is it not? We won't compute the fractions affected by the CPU, due to the rather obvious lack of relevance in context (staring at zeroes is equally boring).
Now, we're in a position to draw a few conclusions/fit things in a semi-coherent image:
- Cypress is primarily bound by its engine clock, with it having the highest influence on achievable performance
- VRAM bandwidth is less of a limiting factor, but it gains importance for higher levels of AA
Finally, if you look at the fractions shown along the way, they help to outline something that's usually lost in the background noise: graphics represent an intricate lattice of intertwined elements that are bound by different factors, and within the confines of a single frame you can be constrained by engine (and many intra-engine factors), memory or even CPU performance, so dealing in absolutes is definitely not the way to go about it.
The fact that Cypress not as limited by VRAM bandwidth as we initially guessed, at least in its 5870 incarnation, can be (simplistically) explained by games typically having an elevated arithmetic intensity (FLOPs/byte ratio). Whilst both the amount of bytes needed to generate one pixel has been increasing itself, the number of computations needed to get the final colour for that pixel has been increasing at a faster pace. Of course, there's more to graphics rendering than pure FLOPs, but in general the weight of on-GPU operations in rendering workloads has been constantly increasing, so if we substitute FLOPs/byte with GPU ops/byte we're probably closer to a more accurate depiction. That's not to say that bandwidth isn't relevant, with its impact being more pronounced as we move to higher levels of AA - whilst it would be nice to assume perfect colour/Z-compression, and thus AA having no cost in bandwidth or compute, practice indicates that's not quite the case, thus making it quite relevant for such scenarios (look at how the fractions affected by the memory clock increase as we add more AA).
We expect the above to hold for 3D rendering in general, but compute workloads are something of a different affair, and one we'll deal with somewhat later, once drivers and SDKs mature a bit and we get everything in place. We'd not be surprised if many compute kernels will be limited by bandwidth before being bound by Cypress' FLOPs.
A nice and simple way of visualising this would be the custom representation of the Roofline Model [Patterson, Williams, 2008], which seeks to put arithmetic intensity, bandwidth and floating-point performance together on a single 2D graph, which looks something like this:
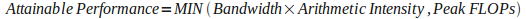

As is obvious, there are a number of simplifications involved, and we're disregarding the impact of caching, taking into account only (theoretical) VRAM bandwidth. On another note, this is an idealised representation: if your nom de plume isn't prunedtree, seeing 2.72 Teraflops from Cypress in actually useful codes is as likely as seeing Dave Baumann crushing his Xbox 360 with a hammer and deleting his Live account.
If we were to place modern game graphical workloads somewhere on that chart, they'd be somewhere to the right, in the [4,16] FLOPs/byte interval - not quite the unachievable pure math nirvana, but not that heavily constrained by bandwidth. We expect games to continue their slow rightward migration in the near future. Compute codes can theoretically be anywhere, but if you're not doing at least more than 2 FLOPs/byte, you may want to consider using the CPU rather than the GPU.
