Compression in general means that we make data smaller, with or without a loss of quality. So can we apply compression to geometry data? To know this we first have to know a bit more about the data required to describe a 3D object and even whole 3d scenes. 

Actually, it seems that the majority of people is unaware of the amount of data that is required to describe a 3D scene. Imagine a single frame in a game. This frame contains, hopefully, nice looking graphics. These graphics were created by the 3D accelerator using a scene description created by the CPU. Basically, you could see it like this: The CPU describes the world and the 3D accelerator makes an image based on that description. Now the big question is, how do we describe such a scene? 

Well as most of you probably know, we use triangles to describe the 3D world. Every object you see on your screen has been described using triangles (or polygons but a polygon can be constructed from one or more triangles). A triangle is actually the simplest 3D object you can describe (using simple vertices). After all, if you use only 2 points you don't really have a 3 dimensional object (a line can be seen as 2D object in 3D space, not so useful to describe volumetric objects). So what we need is some way to describe triangles in 3D space. A 3 dimensional space has 3 coordinates and usually we identify those 3 coordinates relative to an axis. Generally these axis are know as X, Y and Z. So for every vertex we need 3 numbers to indicate where a vertex is in 3D space, relative to the axis selected. Now the next question is, how large are those numbers? Do we need a number from 1 to 10, or what? Well computers describe everything using bits, so a better question would be: how may bits do we want to use to describe a point in 3D space? We could, for example, use a single byte for each axis, this means we would have 256 different positions along an axis. That, however, wouldn't allow us much detail. We could use a full floating point number which requires something like 3 to 4 bytes to be stored, giving us a good level of accuracy. But maybe even too much accuracy. Still, lets assume we use 3 bytes per axis. That means we would need 3 times 3 bytes to describe the position of a single vertex in space! A complete triangle would then require 3 times 9 bytes or 27 bytes, a good deal eh? Actually, this is one point where we can introduce "compression." Instead of using full floating-point accuracy we can select a representation that require fewer bits to store. For example, assume we want to store a cube. A cube is rather simple it has 8 vertices equally spread out in space. If we want we can describe a cube with only 1 bit of accuracy along each axis. So basically a cube can either be represented with full floats (3 to 4 bytes) or one single bit... quite a huge difference! Naturally, it's impossible to describe each object using one bit, but in reality we usually don't need full float accuracy, we can down sample to a lower accuracy. Basically what we need to do is this: we take our object and we place it in a grid. Now this grid can be made finer or coarser by changing the number of bits. If we increase the grid points get closer to each other if we reduce the number of bits we get grid points further apart. Now each grid point can be represented by a coordinate and we thus need to snap the object vertices to these grid points. A coarse grid will introduce errors... and that would mean lossy compression. Now the big trick is to find a good number of bits for the grid. Some objects will require many bits (a fine mazed grid) while other objects (like our cube) can be represented using a very coarse grid. So what is the procedure? 


1. Make an object using high accuracy (full floats). 
2. Place the object inside a cube (or box). 
3. Create a grid inside the cube (certain number of bits => more or less grid points).
4. Snap the vertices to the grid points. 
5. Calculate the error (difference between float positions and grid positions). 
6. If the error is small enough stop or reduce the number of bits fro the grid (coarser grid). 
7. If the error is too large, increase the number of bits for the grid (finer mazed grid).
8. Stop if a good result is obtained (error below threshold using lowest possible bits from the grid. 

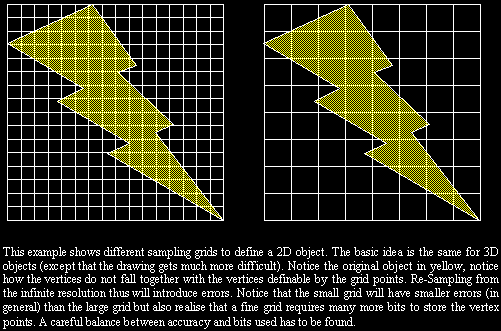
Today we often use full floats; simply because it easy (and because most hardware supports it), but we could save a lot of bits by resampling the geometry to a lower bit depth. Rather complex models can often be stored with just 10 bits of grid detail. This gives us a nice compression ratio. Of coarse this compression is not lossless: some vertices will move due to the snapping to grid points. This mapping can result in the loss of small surface detail. One major problem with this technique is object with variable surface detail. Take for example a car some of the surfaces are really simple and smooth while other parts are highly detailed (e.g. a bolt). Now if we would try to compress this object as one whole, we would either use way to much detail for the simple surfaces or too little detail fro the details which means loss of quality. The best solution is to split these objects up in sub-objects: parts with little details and parts with many fine details should be separated. 

The main disadvantage with this technique is that it has to be supported by the software. You can't re-sample geometry on the fly in hardware. This means that companies, like NVIDIA and S3, that support geometry acceleration and vertex buffers in their hardware will need to push these techniques with software developers. These changes also take time.