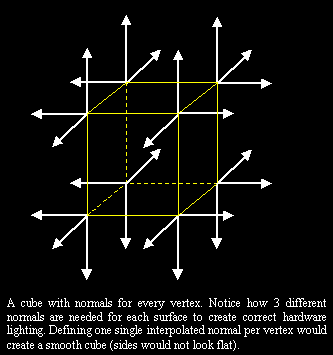
So, again, how many bytes do we want to use to describe those normals? We could use only 1 byte, but again, we could also use 3 bytes. It all depends on accuracy as I explained for the vertices. But lets assume we are happy with 1 byte, naturally one bytes per axis (our normal is a 3D vector). This means that we again need 1 byte times 3 which equals 3 bytes per vertex. For a triangle that adds 9 bytes. Another trick used for normals are look-up tables. We store a certain amount of possible normal directions in a table and we use a pointer towards this table. This might allow us to use only 1 byte per vertex. This does reduce the possible normal directions to only 256. So while we only need one third of the data, we also lose lighting accuracy. Its a trade off, use a lot of space or get less accuracy.
So now we have an object with normals, but no color. Our object must have a color, so this is where vertex colors come in. A vertex color is a color that is attached to a vertex of a triangle, the points inside the triangle get a color based on the colors at the vertices, and we get smooth interpolations. So how many bytes do we want to use to describe that color? Well we could use 16-bits or 32-bits of color. After all, we could also make the triangle transparent by defining an alpha value (RGBA 32-bits)... With all this talk about 32-bit color being important, lets use 32-bits or 4 bytes. Now that adds 4 bytes per vertex, or 12 bytes per triangle. Still keeping count of the maximum/minimum number of bytes needed per triangle (don't forget you need many triangles to form an object)?
Ok so now we have a colored a lit triangle. So about textures? How can we add a texture? Well first, we need some way to say what texture we use. So we need a number that acts as a pointer towards a texture we want to use. Assume we use 16-bits, allowing us to use 65,536 different textures. That should be enough. That means there are 2 bytes per triangle. But wait, we use multi-texturing. So we need two (at "least" two) pointers, which thus makes 4 bytes per triangle. Naturally, we could use fewer bytes, but that increases the risk that a game might run out of texture pointers. Because of this, most hardware and software drivers play safe.
Ok, now we know what textures to use. We just don't know how to stick it to the surface of our triangle. To know how to map a 2D picture on a 3D triangle we need texture coordinates. Texture coordinates are numbers that link a vertex to a point in the 2D map. So it's kind of like snapping each vertex to a point in the 2D texture. The texture then stretches and deforms to match all the 3 vertices to its texture coordinates. Now how many bytes do we need for those texture coordinates (usually these coordinates are identified as UV coordinates)? Well usually, these numbers are again expensive floats. But lets just say we need only 2 bytes for every axis (2 axes needed as we are giving coordinates in a 2D texture map). So that would be 2 times 2, being 4 bytes per vertex, or another 12 bytes per triangle. But wait, we had TWO texture maps. So 24 bytes per triangle. Getting worried already about our maximum (and minimum) number? Also keep in mind that we might want more than 2 textures. Some people would love to see 8 textures per triangle. Maybe they will reconsider that opinion after reading this.
We still need some other things, like what blending mode (how to combine textures) are we using for the textures? And even more what kind of mapping do we use: clamp, mirror, border, ... we need another set of bytes to give the hardware more info about how to use and combine those texture maps. So add about another byte per triangle (maybe even more) to give the hardware some clue on what to do.
I think we now have it... let's add it all up, all per triangle worst (well not completely worst, I already cut it some slack) uncompressed case:
Vertex Coordinates in 3d Space = 27 bytes
Vertex Normal = 9 bytes
Vertex Color = 12 bytes
Texture Pointer = 2 bytes
Texture coordinates = 24 bytes
Parameters = 1 byte
Grand Total of 75 bytes for a single triangle. That's not even the very worst case! I could have used a much higher accuracy for the vertex normals, also for the texture coordinates, not to mention that more parameters might be needed. But lets say we use 75 bytes. 75 bytes for one single triangle. Doesn't sound like much does it? Well it is a lot because you need to remember that the AGP bus only shifts 64 bits per clock. That's 8 bytes. You thus need more than 9 transfers to get that data to the 3d card... 9 AGP clocks... for a single triangle. So how much bandwidth do we need for say 2 million triangles? 2 Million times 75 bytes is 150 MB of triangle information. Still doesn't sound like that much, but AGP bandwidth is shared bandwidth. The AGP system makes use of a bus that is used by the CPU, memory and all PCI devices. So all-in-all with this concurrent use, collision, etc. Who says we can handle 150 Mb/sec? It doesn't seem that bad until you consider that a year from now games will be using considerably more triangles than that. Expect 10-15 million. Assuming we do 15 million, 15 million x 75 bytes equals 1.125 Gb/sec. That's even more than an AGP bus has! And lets not forget this AGP bus is shared. The CPU needs data, your PCI sound card is using local memory to store and play sounds. Also, lets not forget about textures stored in system memory. All of this is using bandwidth. Can we really handle such a data stream?
Naturally there are some solutions to this problem. First of all, I told you that we could use compression. We can bring our vertex coordinates from 27 bytes to about 12 bytes by using grid re-sampling. The vertex normals can be placed in a look-up table. For example, 8 bits per vertex normal so only 3 bytes from the original 9. The vertex color might also use a lookup table (point to a small color table - some hardware might support this) so maybe again only 1 byte per vertex, 3 bytes per triangle from the original 12 bytes. We could also stick to 16-bit vertex colors, which would mean 6 bytes instead of 12 bytes. Texture pointers... we could reduce the amount of textures, but its a risk. For texture coordinates I already used a rather competitive number in the original discussion. So lets make a new grand total, lets call this a more optimal case:
Vertex Coordinates in 3d Space = 12 bytes (27 bytes)
Vertex Normal = 3 bytes (9 bytes)
Vertex Color = 3 bytes or 6 bytes (12 bytes)
Texture Pointer = 2 bytes
Texture coordinates = 24 bytes
Parameters = 1 byte
A new total of 45 bytes (or 48 bytes depending on the vertex colors). It's a nice reduction and I am sure that we could even reduce some things like the texture coordinates. E.g. assume we only support single texturing, that would reduce the number with another 12 bytes, or maybe we can downsample that accuracy too? Exact numbers are hard to quote... these numbers given here are just for illustration, I can't guarantee that they are 100% correct, but I assume they are an acceptable guess. If you know more, feel free to email or post in the forum.
But now on to another and better known solution: use strips and fans. As you probably know, strips and fans re-use vertices for several triangles. In theory, you can define a new triangle by only supplying one vertex. So in theory, your bandwidth can be reduced to only one third. I would say that using strips and fans is pretty damn essential for T&L hardware performance. In case you don't know how strips work, take a look at the graph below. Notice how you can go from one triangle to another neighboring triangle and notice that neighbors have 2 vertices in common, so you add a new vertex and you re-use two old ones.
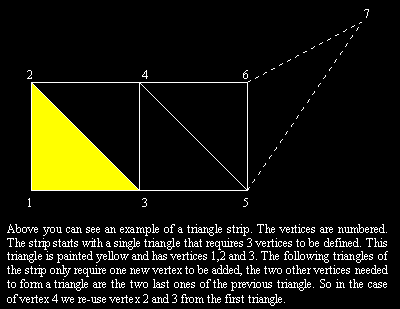
A strip, however isn't perfect. You can't use one huge strip for the scene- you can't even use one strip to build a single object. Strip lengths are limited (e.g. Quake use a strip length of 10). But even then, while you can save some information with strips, there is no guarantee that the whole bandwidth is reduced to one third. What about different texture coordinates and textures for the various triangles that share a strip vertex? All-in-all, some very theoretical studies have shown that on average a vertex to triangle ratio of 1.6 can be obtained. So that means half the bandwidth... but with exceptions... texture coordinates can only be shared if they are the same (the same texture is used), the same is true for other things like vertex colors and also for normals (as I pointed out with the cube)... so even with strips, you still keep a lot of data. But even then, the amount of bandwidth over the AGP bus is large. It is no wonder that companies like NVIDIA have been pushing AGP x4 and Fast Writes. They can use every byte they can get.
There is a way to expand strips to even higher savings, by using an on-chip vertex cache. If we were to look at an object, we would see that there are several strips laying on top of each other (one at the top, one under it, etc.). Now while the triangles in one such strip share vertices we also note that the strips themselves are sharing vertices. Now by using a vertex cache on the chip we can also re-use these vertices. This allows us to reach up to 0.6 vertices per triangle! Do keep in mind that this is a rather new technique that requires special hardware and software support. The software model has to support this cache and the hardware has to have an on-chip buffer for vertices.
Note that this is just an overview of the data that you need. All data members mentioned above can be needed to form and describe a 3D object using triangles. How many bytes are used for every member is under discussion. OpenGL allows the coder the choice between various sizes going from full precision floating points to sizes below a single byte, based on wanted accuracy. OpenGL allows vertex and normal data compression techniques as we described above. Today, the choice for the data type has to be made by the application, and very often the coders use full floating point precision because they think its best. But its obvious that in terms of bandwidth, this is not a wise choice (in terms of visual accuracy it is).
