Fun with your Vertex Friends…
So here we are with our vertex in 3D space, what can we do with our new little friend? Well we could move him, he has been comfortably in that spot for too long let’s shift him around a bit:
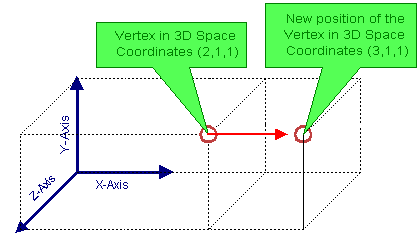
In the figure above we moved our little friend to the right, we could have moved him to the left, or up, or down, forwards or even backwards. All of this is known as translations, we move our vertex to a new position. A new position means that new distances come into play relative to our Cartesian Coordinates System. Rather than talk about a distance we usually just give numbers, to be able to link distance to numbers you need a base unit, you can select this in anyway you want whatever distance you like you declare 1, any other distances will be relative to the length you declared to be 1. So using this we can say that our vertex was at (x,y,z)=(2,1,1) and we moved him to (x,y,z)=(3,1,1). So how can we define this using mathematic, well all we did is add 1 unit to the X-value : X’=X+1, we left the other values, Y and Z alone : Y’=Y and Z’=Z. So a translation seems to be nothing more than an addition. Now what happens if we add a value to a group of vertices that form a cube?
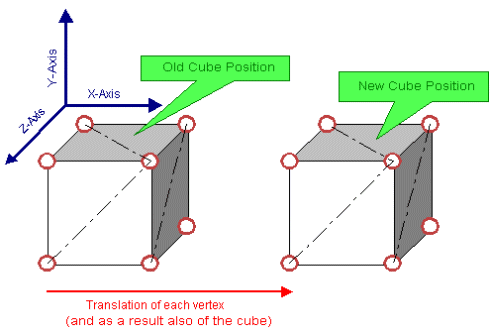
As said before what we do to a vertex will happen to a triangle, what happens to a triangle happens to the whole object formed by the triangles. So when our vertex moves to the right, so does the triangle and obviously also the whole cube. A Translation is the first type of Transformation that we have discovered, we transformed our vertex, triangle, object to a new position.
Now what else can we do with our vertex, well we “added†a value to a coordinate why not try and “multiply†the value of a coordinate and see what happens? Lets do this X’=X*2, Y’=Y and Z’=Z :
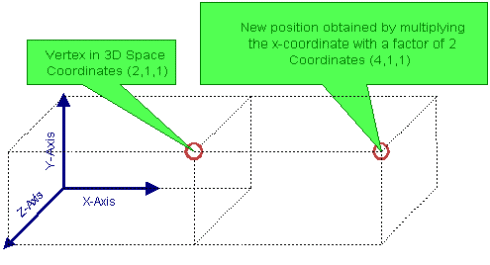
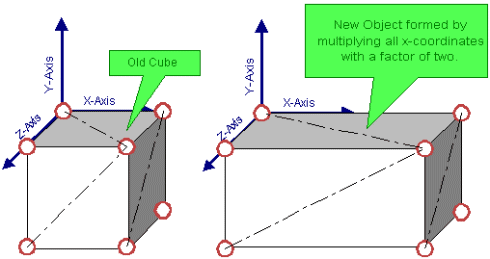
Ah, now things are clear, we now have a cube which is twice as big in the X-direction, the Y and Z direction remained the same. We have managed to find a new transformation: Scaling. Obviously we could have made things more exciting by scaled along all the axes using different ratios, we could even have added a translation to the whole thing.
