Now what else can we do, how about a rotation? The maths to do those involve sine and cosine which is a bit complicated so just trust me. We can rotate our little friend around the Z-axis:



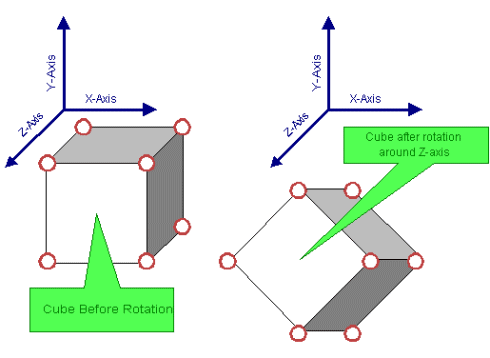
And obviously we can do the same with all his friends that form the cube:

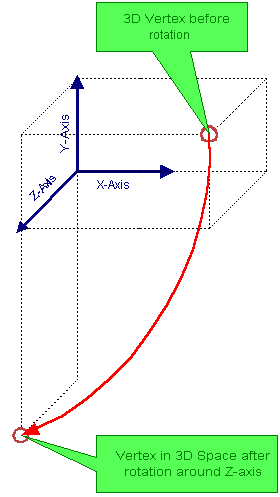
This is our third transform: the Rotation. But this is not the end; it is just the start since you can do anything you want to our little vertex friend’s position. Do you want to take his square root? Multiply the X and Y coordinate and put it in the Z coordinate? Add X, Y and Z coordinate, raise it to a power, divide by the sine of the X coordinate, and … and … well you get the idea: you can do anything you want with your little vertex friend and something really exciting might happen to him, and his friends and obviously something will also happen to the triangles and objects that they form together.

All these exotic transformations sound cool, but they might not be immediately functional. The Translation, Rotation and Scaling Transformations are the most used ones. Obviously you have already figured out the use of these transformations within a game. Using these transforms any objects can be moved around in the 3D world: the car driving along the road, the mouse chasing the cat (errr?), etc… transforms make it all possible.

The Matrix, the one that changes the world

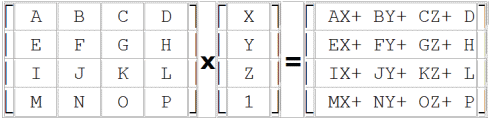
To efficiently execute transformations (and lots of other things) mathematicians invented something called a matrix and on a matrix you can perform various matrix operations. We are mainly interested in the matrix operation that allows us to execute the basic transformations: the matrix product, which is defined as follows:

n the equation shown above you can see on the left of the product the “matrix” (basically a 4 by 4 grid of numbers), on the right of the product you see a set of 4 numbers indicating the position of our vertex (x, y, z coordinates and a 1 added to make it all work). On the right side of the equation you see the result of the transformation. Notice how its perfectly possible to create a translation, for example if we want to translate the x coordinate of our vertex we only need to add the translation value to position 4 of our matrix, since X’ = AX+BY+CZ+D, if position A of the matrix equals 1 and positions B and C equal 0 then the formula becomes: X’ = X + 4. So the value of matrix position D gets added to the X coordinate.

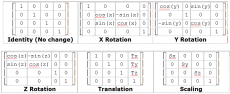
All other basic transformations can be done using this matrix representation:

One thing to note is that weird exotic transformations of coordinates are not possible using the matrix representation. So if you want a transformation that expresses that X’=sine(X) + cosine(Y) + Z3 then you’ll have to look elsewhere.